The Proportional Relationships and Slope Worksheet is an invaluable resource that provides a thorough exploration of these fundamental mathematical concepts. It offers a comprehensive overview, engaging activities, and real-world applications, making it an essential tool for students and educators alike.
This worksheet delves into the nature of proportional relationships, explaining the concept of slope as a measure of the relationship’s steepness. Through a series of interactive activities, students will gain a deep understanding of how to solve proportions, graph proportional relationships, and apply these principles to solve real-world problems.
Proportional Relationships and Slope
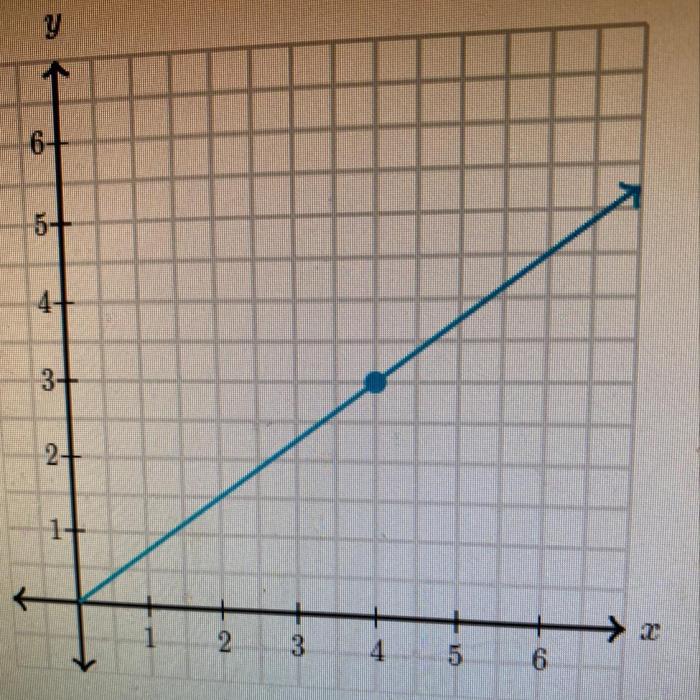
Proportional relationships describe a linear relationship between two variables where one variable increases or decreases at a constant rate relative to the other. Slope, a crucial concept in proportional relationships, quantifies this rate of change and provides valuable insights into the behavior of the relationship.
Understanding proportional relationships is essential in various fields, including mathematics, science, economics, and engineering. They enable us to make predictions, solve problems, and analyze data effectively.
Worksheet Activities
The worksheet includes a series of activities designed to enhance students’ understanding of proportional relationships and slope:
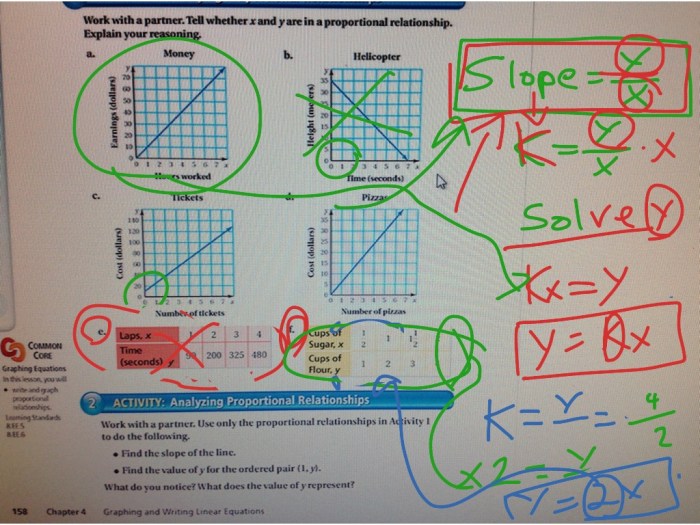
- Identifying Proportional Relationships:Students analyze data tables and graphs to determine if relationships are proportional and justify their reasoning.
- Calculating Slope:Students practice calculating the slope of proportional relationships using the slope formula and real-world examples.
- Graphing Proportional Relationships:Students plot points and draw graphs to represent proportional relationships, observing the relationship between slope and the steepness of the graph.
- Applications in Real-World Scenarios:Students explore real-life situations where proportional relationships are applied, such as speed-distance relationships and constant rates of change.
Solving Proportions, Proportional relationships and slope worksheet
Solving proportions involves finding the value of an unknown variable in an equation where two ratios are equal. The steps involved are:
- Cross-multiply the numerators and denominators of the ratios.
- Solve the resulting equation for the unknown variable.
| Proportion | Cross-Multiplication | Solution |
|---|---|---|
| a/b = c/d | ad = bc | a = bc/d |
Graphing Proportional Relationships
Proportional relationships can be graphed using the slope-intercept form: y = mx + b, where:
- y is the dependent variable
- x is the independent variable
- m is the slope
- b is the y-intercept
The slope determines the steepness of the graph and represents the rate of change in the dependent variable relative to the independent variable.
- Positive slope:The line rises from left to right.
- Negative slope:The line falls from left to right.
- Zero slope:The line is horizontal.
- Undefined slope:The line is vertical.
Applications of Proportional Relationships
Proportional relationships have numerous applications in real-world scenarios, including:
- Science:Determining the relationship between temperature and volume, or force and acceleration.
- Economics:Calculating the relationship between supply and demand, or income and expenditure.
- Engineering:Designing structures that withstand forces, or determining the efficiency of machines.
By understanding proportional relationships, we can make informed decisions, solve problems, and gain insights into the behavior of complex systems.
Common Queries: Proportional Relationships And Slope Worksheet
What is the concept of proportional relationships?
Proportional relationships describe a constant ratio between two variables, meaning that as one variable increases, the other increases proportionally.
How is slope calculated in a proportional relationship?
Slope is the ratio of the change in the dependent variable to the change in the independent variable, representing the steepness of the relationship’s graph.
What are some real-world applications of proportional relationships?
Proportional relationships are used in various fields, including science, economics, and engineering, to model relationships between variables such as distance and time, price and quantity, or force and acceleration.